점프와 순간 이동
문제 링크 : https://school.programmers.co.kr/learn/courses/30/lessons/12980
문제에 대한 내용
문제 설명
OO 연구소는 한 번에 K 칸을 앞으로 점프하거나, (현재까지 온 거리) x 2 에 해당하는 위치로 순간이동을 할 수 있는 특수한 기능을 가진 아이언 슈트를 개발하여 판매하고 있습니다. 이 아이언 슈트는 건전지로 작동되는데, 순간이동을 하면 건전지 사용량이 줄지 않지만, 앞으로 K 칸을 점프하면 K 만큼의 건전지 사용량이 듭니다. 그러므로 아이언 슈트를 착용하고 이동할 때는 순간 이동을 하는 것이 더 효율적입니다. 아이언 슈트 구매자는 아이언 슈트를 착용하고 거리가 N 만큼 떨어져 있는 장소로 가려고 합니다. 단, 건전지 사용량을 줄이기 위해 점프로 이동하는 것은 최소로 하려고 합니다. 아이언 슈트 구매자가 이동하려는 거리 N이 주어졌을 때, 사용해야 하는 건전지 사용량의 최솟값을 return하는 solution 함수를 만들어 주세요.
예를 들어 거리가 5만큼 떨어져 있는 장소로 가려고 합니다.
아이언 슈트를 입고 거리가 5만큼 떨어져 있는 장소로 갈 수 있는 경우의 수는 여러 가지입니다.
- 처음 위치 0 에서 5 칸을 앞으로 점프하면 바로 도착하지만, 건전지 사용량이 5 만큼 듭니다.
- 처음 위치 0 에서 2 칸을 앞으로 점프한 다음 순간이동 하면 (현재까지 온 거리 : 2) x 2에 해당하는 위치로 이동할 수 있으므로 위치 4로 이동합니다. 이때 1 칸을 앞으로 점프하면 도착하므로 건전지 사용량이 3 만큼 듭니다.
- 처음 위치 0 에서 1 칸을 앞으로 점프한 다음 순간이동 하면 (현재까지 온 거리 : 1) x 2에 해당하는 위치로 이동할 수 있으므로 위치 2로 이동됩니다. 이때 다시 순간이동 하면 (현재까지 온 거리 : 2) x 2 만큼 이동할 수 있으므로 위치 4로 이동합니다. 이때 1 칸을 앞으로 점프하면 도착하므로 건전지 사용량이 2 만큼 듭니다.
위의 3가지 경우 거리가 5만큼 떨어져 있는 장소로 가기 위해서 3번째 경우가 건전지 사용량이 가장 적으므로 답은 2가 됩니다.
제한 사항
- 숫자 N: 1 이상 10억 이하의 자연수
- 숫자 K: 1 이상의 자연수
입출력 예
| N | result |
|---|---|
| 5 | 2 |
| 6 | 2 |
| 5000 | 5 |
입출력 예 설명
입출력 예 #1
위의 예시와 같습니다.
입출력 예 #2
처음 위치 0 에서 1 칸을 앞으로 점프한 다음 순간이동 하면 (현재까지 온 거리 : 1) x 2에 해당하는 위치로 이동할 수 있으므로 위치 2로 이동합니다. 이때 1 칸을 앞으로 점프하면 위치3으로 이동합니다. 이때 다시 순간이동 하면 (현재까지 온 거리 : 3) x 2 이동할 수 있으므로 위치 6에 도착합니다. 이 경우가 건전지 사용량이 가장 적으므로 2를 반환해주면 됩니다.
입출력 예 #3
위와 같은 방식으로 합니다.
접근 방식
- dfs를 사용해서, 모든 경우의 수를 돌면서 값을 구하도록 했다.
잘못된 접근
import java.util.*;
public class Solution {
static int answer = Integer.MAX_VALUE;
public int solution(int n) {
dfs(n, 0, 0);
return answer;
}
private void dfs(int n, int idx, int cnt){
if(idx > n) return;
if(idx==n) {
answer = Math.min(answer, cnt);
return;
}
dfs(n, idx+1, cnt+1);
if (idx!=0) dfs(n, idx*2, cnt);
}
}

하지만 테스트 결과.. 주어진 N의 값이 작은 경우에는 쉽게 통과과 됐지마느 N의 크기가 커지는 경우 재귀가 증가하면서 실행 시간이 비정상적으로 증가하게 되었다..
로직을 변경해야 했다.
일단 중간에 현재 cnt가 answer보다 크면 return 하도록 추가했다.
if(idx > n || cnt > answer) return;
잘 된 접근
코드를 변경했지만, 아직도 효율성 테스트를 통과하지 못했다…
N이 최대 10억까지 주어지다 보니, 일정 숫자를 벗어나는 경우 오버플로우가 발생하여 문제가 생긴 것 같다.
코드에 혁신이 필요한 것 같다..
아무래도 완전 탐색으로 푸는 문제는 아닌 것 같다.
이런 문제의 경우, 규칙이 존재하는 경우가 있으니 규칙을 찾아보도록 하자.
간단하게 1부터 5까지 직접 해 보자!
1부터 10까지 직접 계산해 본 결과, 규칙이 존재했다.
- 1 => 1
- 2 => 1
- 3 => 2
- 4 => 1
- 5 => 2
- 6 => 2
- 7 => 3
- 8 => 1
- 9 => 2
- 10 => 2
여기서 규칙은 N이 짝수일 경우에는, N 나누기 2의 결과와 값이 동일하다는 것이다. (1==2==4==8)
그리고 홀수인 경우에는, 1을 빼고 나누기 2를 한 값에 +1을 하면 결과 값이 나온다. (N=9, 9-1=8 => 8/4 => 4/2 => 2/2 => 1+1 => 2)
이 규칙을 통해 알 수 있는 것은, 백트래킹을 통해 거꾸로 쭉 알아가다 보면 결국에 값이 구해진다는 것이다.
홀수인 경우에는, 1을 빼주고(cnt+1), 짝수의 경우에는 /2 를 한다. 그렇게 최종 값이 0에 도달할 때까지의 cnt의 값을 구하면 그것이 바로 최종 결과 값이 된다는 것이다.
이를 코드화 해보자!!
while(n>0){
if(n%2==0) n/=2;
else {
n--; cnt++
};
}
위와 같이 간단한 코드가 나온다.
- 현재 n이 짝수일 경우, 계속 2로 나눈 몫으로 n을 변경하고,
- n이 홀수인 경우, 1을 빼고, cnt를 +1 해준다.
- 그렇게 계속 코드를 돌다가, n이 0보다 작거나 같아지면 while문을 빠져나오게 된다.
이제 위 알고리즘을 원본 코드에 넣어주고 cnt를 리턴해주면 된다.
결과
소스 코드
import java.util.*;
public class Solution {
public int solution(int n) {
int cnt = 0;
while(n>0){
if(n%2==0) n/=2;
else {
n--;
cnt++;
}
}
return cnt;
}
}
결과 이미지
효율성 테스트를 가볍게 통과했다.
실제로 이전 코드의 정확성 테스트의 일부를 보면
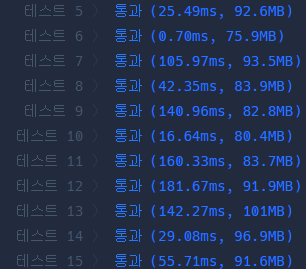
일반적으로 10ms대 속도가 나오고, 많이 나오는 경우 100ms대가 나오는 것을 확인할 수 있다.
재귀로 인해 기하급수적으로 시간 복잡도가 증가하기 때문이다.
바뀐 코드는 시간 복잡도가 O(n)에 해당하기 때문에, 굉장히 빠른 속도를 자랑한다.
다른 접근 방식
다른 사람의 풀이를 보다가, 깜짝 놀랐다. 바로 코드가 리턴을 제외한다면 없기 때문…….
이럴 수가..
return Integer.bitCount(n);
위의 코드를 사용하고 있었다. n을 비트로 변환했을 때 1의 갯수를 리턴하고 있다.
어이가 없었다.
왜 이렇게 답이 나오는지 궁금해서, 퍼플렉시티에게 물어봤다.
이해가 안 됐다.
그냥 나와는 다른 세계라고 생각하고 이런 방식도 있구나하고 이해해야 할 것 같다.
알게 된 점
완전 탐색으로 풀어보다가,
풀리지 않는다면 일정 숫자(혹은 횟수) 만큼 직접 답을 구해보고
그 사이에서 규칙을 찾아볼 것!
완전 탐색으로 풀리지 않는다면 반드시 규칙이 존재한다는 뜻!!