피보나치 수
문제 링크 : https://school.programmers.co.kr/learn/courses/30/lessons/12945
문제에 대한 내용
문제 설명
피보나치 수는 F(0) = 0, F(1) = 1일 때, 1 이상의 n에 대하여 F(n) = F(n-1) + F(n-2) 가 적용되는 수 입니다.
예를들어
- F(2) = F(0) + F(1) = 0 + 1 = 1
- F(3) = F(1) + F(2) = 1 + 1 = 2
- F(4) = F(2) + F(3) = 1 + 2 = 3
- F(5) = F(3) + F(4) = 2 + 3 = 5
와 같이 이어집니다.
2 이상의 n이 입력되었을 때, n번째 피보나치 수를 1234567으로 나눈 나머지를 리턴하는 함수, solution을 완성해 주세요.
제한 조건
- n은 2 이상 100,000 이하인 자연수입니다.
입출력 예
| n | return |
|---|---|
| 3 | 2 |
| 5 | 5 |
입출력 예 설명
피보나치수는 0번째부터 0, 1, 1, 2, 3, 5, … 와 같이 이어집니다.
접근 방식
- F(0)과 F(1)을 미리 정의한다.
- 조건이 2<=n<=100000 이기 때문에, 2부터 시작해서 n번째의 피보나치 수만 알면 된다.
- 따라서 이전 수들을 저장할 필요가 없다.
잘못된 접근
class Solution {
public long solution(int n) {
long answer = 0;
long tmp1 = 0;
long tmp2 = 1;
long tmp3 = 0;
for (int i=2; i<=n; i++){
tmp3 = tmp1 + tmp2;
tmp1 = tmp2;
tmp2 = tmp3;
if (i==n) answer = tmp3;
}
return answer % 1234567;
}
}
제출 후에, 일부 테스트만 통과하고 나머지는 실패했다.
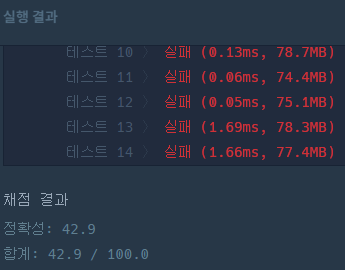
분명히 코드에서 틀린 점은 없는데, 무엇이 문제일지 생각해보았다.
피보나치 수열의 수 증가를 간과하고 있었다.
주어진 int 타입의 수치를 벗어날 것으로 예상하여 long 타입으로 지정하였으나, 이것도 n=93일 경우 long 타입의 최대 수인 약 1,000경을 넘어선다.
따라서, n이 93이상 인경우, 오버헤드가 발생하여 최종 값에 근접하지 못한다.
그래서 사전에 모듈러 연산을 하여 값을 최소화 시켰어야 했다.
결과
소스 코드
class Solution {
public int solution(int n) {
int answer = 0;
int tmp1 = 0;
int tmp2 = 1;
int tmp3 = 0;
for (int i=2; i<=n; i++){
tmp3 = (tmp1 + tmp2) % 1234567;
tmp1 = tmp2;
tmp2 = tmp3;
if (i==n) answer = tmp3;
}
return answer;
}
}
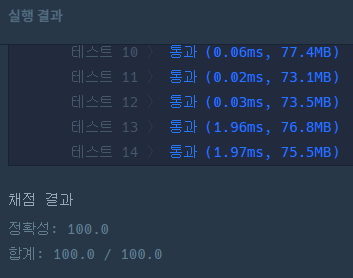
어차피 모듈러 연산의 결과 값은, 120만을 넘어서지 않는다.
따라서 타입을 int형으로 지정해도 괜찮다.
결과 이미지
알게 된 점
어차피 나눠야 한다면, 미리 나눠서 데이터의 크기를 줄이자!